
1, we can see that the negative value of the coefficient shifts the curves in the positive x-axis and negative f(x)-axis if the coefficient is positive, while shifts to the negative x-axis and positive f(x)-axis if the coefficient is negative. 3 of the quadratic function equations of (red solid curve) and (blue solid curve), and if we compare this graph with the graphs in Fig. Similarly, if we see the below graphs in Fig. 1, we can see that the positive value of the coefficient shifts the curves in the negative x-axis and negative f(x) -axis if the coefficient is positive, while shifts to the positive x-axis and positive f(x)-axis if the coefficient is negative.įigure 2: Graph of the functions, in the red and blue solid curves, respectively. 2 of the quadratic function equations of (red solid curve) and (blue solid curve), and if we compare this graph with the graphs in Fig. Therefore, if we see the below graphs in Fig.
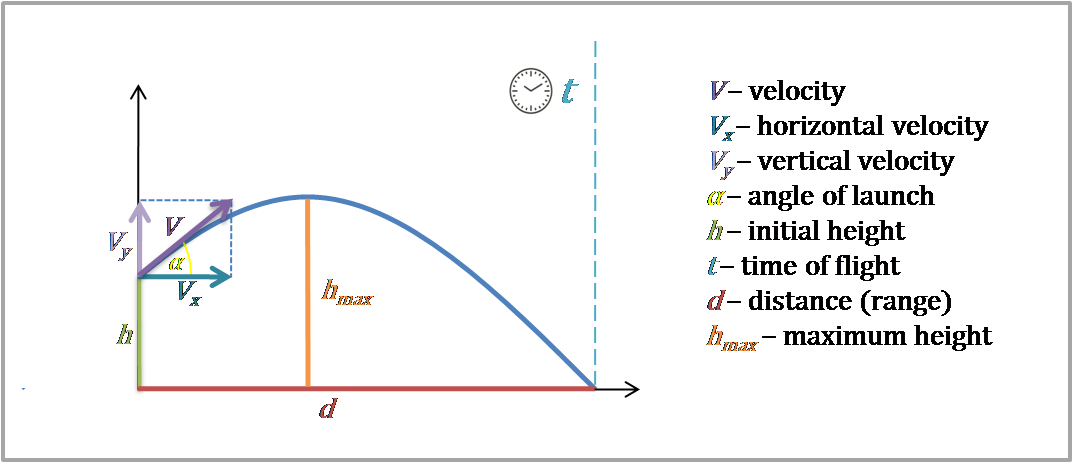
In the below graphs the quadratic function equation, gives an upward curve (solid red curve), while the equation gives a downward curve (solid blue curve), therefore the sign of the coefficient in the quadratic function equation determines the direction of the opening of the parabola.įigure 1: Graph of the functions, in the red and blue solid curves, respectively.įurther, if we see the graphs, where we have added another term such that the quadratic function equations become in the form of, Is positive, then it gives an upward curve (towards the positive axis) while if it is negative then it gives a downward curve (towards the negative axis). Since the variable can not be zero, therefore, we can make the graphs of the function, Therefore, we can define the shape of the quadratic function equations using the standard form of the quadratic function equations.įigure: The vertex and axis of symmetry of the parabolaįor the case, when variables are equal to zero. The vertex and axis of symmetry of the parabolic curve are defined in the below graph. Since the quadratic function equations have at least one of their variables with the power of the exponent equal to 2 therefore the quadratic function equations are given in the shape of the parabola, which is always symmetric about a given axis of symmetry and has one vertex. The role of the constants in shaping the graph of the quadratic function Some examples of quadratic function equations are, The standard form of the equation is used to generalize the outcome of the given quadratic function equations. Where can have the values of any real number except The standard form of the quadratic function equation can be expressed as, The standard form of the quadratic function equation Looking to Learn Math? Explore Wiingy’s Online Math Tutoring Services to learn from top mathematicians and experts. In the launch of a rocket, its trajectory can be predicted by the simple quadratic function equation, isn’t it fascinating? The other uses of the quadratic function involve the calculation of speed, the area under the curve, an estimate of the projectile motion of any object, and the loss and profit in the area of economics. The quadratic function equation is important because of its practical applications in daily life. A quadratic equation is a form of the algebraic equation, that is intrinsically defined in the form of, and therefore, this function maps the points which can be defined with the coordinates. In other words, among the all variables in the equation if any of them has a maximum exponent value equal to two, then that equation is called the quadratic equation. The highest value of the exponent is two therefore the equation is called the quadratic equation.

The quadratic function equations are such polynomial equations that can be either of one variable and/or more than one variable, where the maximum value of the exponent of any variable is not more than two.


 0 kommentar(er)
0 kommentar(er)
